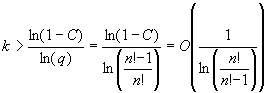James Caristi

Valparaiso University

Dick Botting described the "Las Vegas Sort" as follows:

He claimed that this "algorithm" was O(n!), and was good for a laugh in class.

As described, the algorithm is not "effective"; that is, it is not guaranteed to terminate in a solution. However, we can change the specifications to allow k iterations, and terminate when the probability that the deck has been sorted at least once in those k iterations is greater than some certainty, C. If we choose k so large that we will be sure the deck is sorted with probability at least C, then we can ask whether k is indeed O(n!) where n is the number of cards in the deck. It is not clear that this is a O(n!) situation, so the following proof is presented.

Let p be the probability that the deck is sorted at the end of any shuffle. Then for n cards, . Letting q = 1 – p, then the probability of k consecutive failures is . We want to find k such that the probability of having at least one success in k shuffles is at least C where 0 < C < 1. This is equivalent to saying that we seek k such that the probability that all k shuffles result in failure is less than 1 – C. Therefore we want k so large that . Taking logs of both sides and using the fact that q < 1 means ln(q) < 0, we obtain 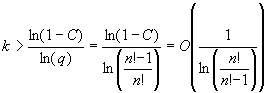(using the fact that ln(1 – C) is negative and the choice of C is independent of n). To determine whether this is O(n!), we have to examine the behavior of near x = 1.

Consider the function . Not only do both f(x) and g(x) approach infinity as x approaches 1, but also . Hence f and g are asymptotically equivalent near 1. Replacing x by we obtain 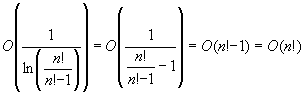.