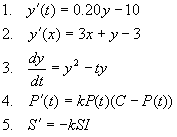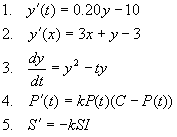
(In the last example, the independent variable t is understood)

"The rate at which population changes depends on [is proportional to] the size of the population and how far the population is from carrying capacity" This is example 4 above.

"The susceptible population changes at a rate that is proportional to the number of contacts between susceptible and infective individuals". This is example 5 above.

"A fish population increases at a continuous rate of 20% per year, and the fish are being harvested at a constant rate of 10 million fish per year". This is example 1 above.

What do you mean by a solution to a differential equation? The solution to a differential equation is a function that represents the values of the dependent variable for all values of the independent variable. For all of the "population" examples given above, that means finding the population at all possible points in time. In the particular example 1, the function solves the equation where C is any constant. You should be able to verify that. This means that in fact, there are infinitely many solutions to this equation, one for each choice of C. Notice that in all the "real world" examples in B, there are infinitely many possible population functions, depending on how big the population was to begin with (in other words, it makes a difference whether there are 100 fish or 1,000,000 fish to begin with). This requirement of having to know the population to begin with is called the initial condition. Nevertheless, all of the possible population functions that describe the fish population would look similar – they would be parallel in some sense. We will see this better in the lab.

How do you find solutions to differential equations? With great difficulty. Most differential equations cannot be solved "by formula", but we can always approach the process numerically and/or graphically. In the lab, we will look at a graphical method involving "slope fields". Here is a very simplistic numerical idea that actually forms the basis of almost every advanced numerical technique. The differential equation tells you the slope of the tangent line to the unknown function, and knowing the value of the unknown function at the initial condition lets you estimate the value of the function one small unit to the right by following the tangent line. Try this example. Using the differential equation of example 1 with the initial condition y(0)=60 million fish, at t=0 we find 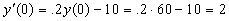. So at time 0 the fish population is growing at a rate of 2 million per year. So at time 1, we can expect the fish population to be about 62 million, or y(1)=62. Now, knowing this, we can compute the rate of change at time 1, which is 0.2y(1)-10=12.4-10=2.4. So that gives us an estimated population of 62 + 2.4 = 64.4 million fish after 2 years. You should be able to continue this to obtain an estimated population of 67.28 million fish after 3 years.